L’objectif de cet article est de présenter une application des algorithmes génétiques afin de résoudre le problème du voyageur de commerce.
Présentation des algorithmes génétiques
Les algorithmes génétiques s’inspirent de la théorie de l’évolution des espèces. Comme dans la vie, les espèces peuvent se reproduire pour créer de nouveaux individus, et leur ADN peut subir des mutations au cours de leur vie. De plus, à l’instar de ce qu’on observe dans la nature, plus un individu est “fort”, plus il a de chance de se reproduire.
Un algorithme génétique est constitué de 5 grandes étapes que nous détaillerons par la suite lorsque nous résolverons notre problème du voyageur de commerce :
- Création d'une population initiale
- Evaluation de la "fitness" (qualité) des individus
- Création de nouveaux individus
- Ajout des nouveaux individus dans la population
- Retour à la seconde étape
Le but de l’algorithme génétique est de faire évoluer notre population initiale vers une population contenant de meilleurs individus.
Application au problème du voyageur de commerce
Le problème du voyageur de commerce consiste à passer par un ensemble de villes en minimisant la distance totale du trajet. C’est un problème dit NP-complet, ce qui signifie qu’il n’existe pas d’algorithme en temps polynomial permettant de trouver une solution exacte à ce problème,.
Commençons par un peu de code. Nous allons créer une classe Ville. Les villes sont définies par leurs coordonnées GPS (longitude et latitude), et leur nom.
class Ville:
def __init__(self, lon, lat, nom):
self.lon = lon
self.lat = lat
self.nom = nom
def distance(self, ville):
distanceX = (ville.lon-self.lon)*40000*math.cos((self.lat+ville.lat)*math.pi/360)/360
distanceY = (self.lat-ville.lat)*40000/360
distance = math.sqrt( (distanceX*distanceX) + (distanceY*distanceY) )
return distancePar la suite nous définissons une classe qui nous permettra de gérer les circuits. Un circuit est caractérisé par un ensemble de villes stocké dans la liste villesDestination. Il est important de mentionner que vu la nature de notre problème, l’ordre des villes a une importance ! Toutefois, un circuit étant une boucle, les circuits Lyon-Paris-Lille-Toulouse et Lille-Toulouse-Lyon-Paris sont équivalents.
class GestionnaireCircuit:
villesDestinations = []
def ajouterVille(self, ville):
self.villesDestinations.append(ville)
def getVille(self, index):
return self.villesDestinations[index]
def nombreVilles(self):
return len(self.villesDestinations)
class Circuit:
def __init__(self, gestionnaireCircuit, circuit=None):
self.gestionnaireCircuit = gestionnaireCircuit
self.circuit = []
self.fitness = 0.0
self.distance = 0
if circuit is not None:
self.circuit = circuit
else:
for i in range(0, self.gestionnaireCircuit.nombreVilles()):
self.circuit.append(None)
def __len__(self):
return len(self.circuit)
def __getitem__(self, index):
return self.circuit[index]
def __setitem__(self, key, value):
self.circuit[key] = value
def genererIndividu(self):
for indiceVille in range(0, self.gestionnaireCircuit.nombreVilles()):
self.setVille(indiceVille, self.gestionnaireCircuit.getVille(indiceVille))
random.shuffle(self.circuit)
def getVille(self, circuitPosition):
return self.circuit[circuitPosition]
def setVille(self, circuitPosition, ville):
self.circuit[circuitPosition] = ville
self.fitness = 0.0
self.distance = 0
def getFitness(self):
if self.fitness == 0:
self.fitness = 1/float(self.getDistance())
return self.fitness
def getDistance(self):
if self.distance == 0:
circuitDistance = 0
for indiceVille in range(0, self.tailleCircuit()):
villeOrigine = self.getVille(indiceVille)
villeArrivee = None
if indiceVille+1 < self.tailleCircuit():
villeArrivee = self.getVille(indiceVille+1)
else:
villeArrivee = self.getVille(0)
circuitDistance += villeOrigine.distance(villeArrivee)
self.distance = circuitDistance
return self.distance
def tailleCircuit(self):
return len(self.circuit)
def contientVille(self, ville):
return ville in self.circuitVous pouvez remarquer que notre circuit contient un attribut fitness et une méthode getFitness. C’est un attribut indiquant la qualité d’un circuit. Dans notre cas, un circuit aura une meilleure fitness lorsque la distance totale sera faible. En effet, l’objectif de notre algorithme est de trouver un circuit minimisant la distance totale de voyage. C’est la raison pour laquelle notre fonction de fitness retourne l’inverse de la distance totale. Ainsi, lorsque la distance diminue, alors la fitness augmente.
Une autre méthode qui mérite quelques précisions est la méthode genererIndividu. Comme nous l’avons expliqué dans la partie précédente, une des étapes principales de notre algorithme est la génération d’une population. Dans notre méthode nous remplissons une liste avec l’ensemble de nos villes puis nous les réordonnons de manière aléatoire en utilisant la fonction random.shuffle.
Nous continuons notre programme par la création d’une classe Population. Dans le cas général, une population est un ensemble d’individus. Dans notre cas cela correspond à un ensemble de circuits.
class Population:
def __init__(self, gestionnaireCircuit, taillePopulation, init):
self.circuits = []
for i in range(0, taillePopulation):
self.circuits.append(None)
if init:
for i in range(0, taillePopulation):
nouveauCircuit = Circuit(gestionnaireCircuit)
nouveauCircuit.genererIndividu()
self.sauvegarderCircuit(i, nouveauCircuit)
def __setitem__(self, key, value):
self.circuits[key] = value
def __getitem__(self, index):
return self.circuits[index]
def sauvegarderCircuit(self, index, circuit):
self.circuits[index] = circuit
def getCircuit(self, index):
return self.circuits[index]
def getFittest(self):
fittest = self.circuits[0]
for i in range(0, self.taillePopulation()):
if fittest.getFitness() <= self.getCircuit(i).getFitness():
fittest = self.getCircuit(i)
return fittest
def taillePopulation(self):
return len(self.circuits)La méthode getFittest nous retourne le circuit ayant la plus grande fitness, ce qui équivaut à la plus faible distance.
Nous allons passer à la création de la classe GA (Genetic Algorithm). Celle-ci contient les principales étapes d’un algorithme génétique :
- L'évolution de la population
- Le crossover
- Les mutations
- La sélection des individus à reproduire
class GA:
def __init__(self, gestionnaireCircuit):
self.gestionnaireCircuit = gestionnaireCircuit
self.tauxMutation = 0.015
self.tailleTournoi = 5
self.elitisme = True
def evoluerPopulation(self, pop):
nouvellePopulation = Population(self.gestionnaireCircuit, pop.taillePopulation(), False)
elitismeOffset = 0
if self.elitisme:
nouvellePopulation.sauvegarderCircuit(0, pop.getFittest())
elitismeOffset = 1
for i in range(elitismeOffset, nouvellePopulation.taillePopulation()):
parent1 = self.selectionTournoi(pop)
parent2 = self.selectionTournoi(pop)
enfant = self.crossover(parent1, parent2)
nouvellePopulation.sauvegarderCircuit(i, enfant)
for i in range(elitismeOffset, nouvellePopulation.taillePopulation()):
self.muter(nouvellePopulation.getCircuit(i))
return nouvellePopulation
def crossover(self, parent1, parent2):
enfant = Circuit(self.gestionnaireCircuit)
startPos = int(random.random() * parent1.tailleCircuit())
endPos = int(random.random() * parent1.tailleCircuit())
for i in range(0, enfant.tailleCircuit()):
if startPos < endPos and i > startPos and i < endPos:
enfant.setVille(i, parent1.getVille(i))
elif startPos > endPos:
if not (i < startPos and i > endPos):
enfant.setVille(i, parent1.getVille(i))
for i in range(0, parent2.tailleCircuit()):
if not enfant.contientVille(parent2.getVille(i)):
for ii in range(0, enfant.tailleCircuit()):
if enfant.getVille(ii) == None:
enfant.setVille(ii, parent2.getVille(i))
break
return enfant
def muter(self, circuit):
for circuitPos1 in range(0, circuit.tailleCircuit()):
if random.random() < self.tauxMutation:
circuitPos2 = int(circuit.tailleCircuit() * random.random())
ville1 = circuit.getVille(circuitPos1)
ville2 = circuit.getVille(circuitPos2)
circuit.setVille(circuitPos2, ville1)
circuit.setVille(circuitPos1, ville2)
def selectionTournoi(self, pop):
tournoi = Population(self.gestionnaireCircuit, self.tailleTournoi, False)
for i in range(0, self.tailleTournoi):
randomId = int(random.random() * pop.taillePopulation())
tournoi.sauvegarderCircuit(i, pop.getCircuit(randomId))
fittest = tournoi.getFittest()
return fittestCette partie du programme demande plus d’explications. Commençons par les attributs de notre classe.
Tout d’abord l’attribut tauxMutation. Comme son nom l’indique, c’est la probabilité qu’une ville d’un circuit subisse une mutation. Dans notre cas, cela correspond à l’inversion de la position de deux villes dans le circuit. Le taux est assez faible car la probabilité d’obtenir une distance plus faible en inversant deux villes est peu élevée.
Type de sélection
L’attribut tailleTournoi correspond à la taille des poules de notre tournoi. Le tournoi est une des méthodes possibles pour sélectionner les individus que nous souhaitons faire se reproduire. Il en existe d’autres telles que la sélection par roulette ou bien la sélection par rang.
Sélection par roulette
Dans le cas de la sélection par roulette, la probabilité qu’un individu soit sélectionné est proportionnelle à sa fitness. C’est à dire que plus un circuit est bon, plus il a de chance d’être sélectionné. L’un des inconvénients de cette méthode de sélection est que si la distribution des fitness n’est pas très uniforme, alors, certains circuits risquent d’être très fréquemment sélectionnés (ceux avec une faible distance) au détriment d’autres circuits (ceux avec grande distance). Or il est important que même les “mauvais” circuits puissent se reproduire.
Sélection par rang
Le principe de la sélection par rang est d’ordonner les individus (ici les circuits) en fonction de leur fitness. La probabilité d’être sélectionné est cette fois proportionnelle au rang de l’individu, et non à sa fitness. Un des problèmes de cette sélection peut être la vitesse de convergence de l’algorithme dans le cas où notre population a très peu de bons individus et beaucoup de mauvais individus. En effet, la probabilité d’être sélectionné pour un bon individu et un mauvais individu ne sera pas très différente. Ainsi, il sera assez fréquent de faire se reproduire des mauvais individus, ce qui peut ralentir la vitesse de convergence de l’algorithme.
Sélection par tournoi
La sélection par tournoi (que nous utilisons) fait affronter plusieurs individus sélectionnés au hasard. Dans notre cas nous organisons des tournois de 5 circuits et nous gardons le circuit avec la distance la plus faible (la fitness la plus élevée). Ainsi, dans le cas où nous faisons s’affronter 5 mauvais individus, cela laisse tout de même une chance à un de ces (mauvais) individus de pouvoir se reproduire.
Elitisme
Dernier attribut : elitisme. Dans un algorithme génétique l’élitisme correspond au fait de vouloir conserver les meilleurs individus d’une génération à une autre, afin d’être sûr de ne pas les perdre. Cela a pour avantage d’accélérer la convergence de l’algorithme au détriment de la diversité des invidus. On peut utiliser diverses formes d’élitisme :
- Copier les n meilleurs individus dans la nouvelle génération
- Sélectionner les n meilleurs individus pour qu'ils se reproduisent
Dans notre cas nous avons choisi la première option, avec un nombre n d’individus égal à 1.
Reproduction des invididus
Jusqu’à présent dans cet article j’ai parlé de reproduction d’individus sans définir ce que j’entendais par reproduction. En effet, qu’entend-on par reproduire deux circuits ?
Dans le cas d’un algorithme génétique on parle souvent de crossover à la place de reproduction. Vous entendrez souvent parler de one/two points crossover.
Expliquons cela plus en détails :
Considérons un single point crossover. Les chromosomes des individus A et B sont définis ainsi :
chr A : 1 0 1 2 1 0 1 0 1 0
chr B : 1 1 0 1 2 1 0 0 2 1
On doit choisir un point de crossover, disons 4 dans notre cas. Cela signifie que de l’indice 1 à 4 notre individu aura les gènes de l’individu A et de l’indice 5 à 10 celui de l’individu B.
L’individu issu de la reproduction de A et B aura donc le profil suivant :
1 0 1 2 2 1 0 0 2 1
Dans le cas d’un two points crossover où l’on choisit les points 2 et 6 cela donnerait :
1 0 0 1 2 1 1 0 1 0
Dans notre cas nous choisissons un two points crossover mais contrairement aux exemples donnés précédemment nous avons une contrainte supplémentaire : la cohérence de notre solution. En effet, l’individu issu de la reproduction doit avoir un circuit contenant toutes les villes possibles. Pour pallier à ce problème nous procédons de la manière suivante :
- On choisit deux indices;
- On recopie les villes présentes entre ces deux indices dans notre futur individu;
- On complète les emplacements vides de notre nouvel individu par les villes manquantes
Résolvons notre problème
Maintenant que nous avons vu l’algorithme à utiliser pour résoudre notre problème du voyageur de commerce, nous allons nous intéresser au code permettant de mettre en oeuvre notre solution.
if __name__ == '__main__':
gc = GestionnaireCircuit()
#on cree nos villes
ville1 = Ville(3.002556, 45.846117, 'Clermont-Ferrand')
gc.ajouterVille(ville1)
ville2 = Ville(-0.644905, 44.896839, 'Bordeaux')
gc.ajouterVille(ville2)
ville3 = Ville(-1.380989, 43.470961, 'Bayonne')
gc.ajouterVille(ville3)
ville4 = Ville(1.376579, 43.662010, 'Toulouse')
gc.ajouterVille(ville4)
ville5 = Ville(5.337151, 43.327276, 'Marseille')
gc.ajouterVille(ville5)
ville6 = Ville(7.265252, 43.745404, 'Nice')
gc.ajouterVille(ville6)
ville7 = Ville(-1.650154, 47.385427, 'Nantes')
gc.ajouterVille(ville7)
ville8 = Ville(-1.430427, 48.197310, 'Rennes')
gc.ajouterVille(ville8)
ville9 = Ville(2.414787, 48.953260, 'Paris')
gc.ajouterVille(ville9)
ville10 = Ville(3.090447, 50.612962, 'Lille')
gc.ajouterVille(ville10)
ville11 = Ville(5.013054, 47.370547, 'Dijon')
gc.ajouterVille(ville11)
ville12 = Ville(4.793327, 44.990153, 'Valence')
gc.ajouterVille(ville12)
ville13 = Ville(2.447746, 44.966838, 'Aurillac')
gc.ajouterVille(ville13)
ville14 = Ville(1.750115, 47.980822, 'Orleans')
gc.ajouterVille(ville14)
ville15 = Ville(4.134148, 49.323421, 'Reims')
gc.ajouterVille(ville15)
ville16 = Ville(7.506950, 48.580332, 'Strasbourg')
gc.ajouterVille(ville16)
ville17 = Ville(1.233757, 45.865246, 'Limoges')
gc.ajouterVille(ville17)
ville18 = Ville(4.047255,48.370925, 'Troyes')
gc.ajouterVille(ville18)
ville19 = Ville(0.103163,49.532415, 'Le Havre')
gc.ajouterVille(ville19)
ville20 = Ville(-1.495348, 49.667704, 'Cherbourg')
gc.ajouterVille(ville20)
ville21 = Ville(-4.494615, 48.447500, 'Brest')
gc.ajouterVille(ville21)
ville22 = Ville(-0.457140, 46.373545, 'Niort')
gc.ajouterVille(ville22)
#on initialise la population avec 50 circuits
pop = Population(gc, 50, True)
print "Distance initiale : " + str(pop.getFittest().getDistance())
# On fait evoluer notre population sur 100 generations
ga = GA(gc)
pop = ga.evoluerPopulation(pop)
for i in range(0, 100):
pop = ga.evoluerPopulation(pop)
print "Distance finale : " + str(pop.getFittest().getDistance())
meilleurePopulation = pop.getFittest()
#on genere une carte représentant notre solution
lons = []
lats = []
noms = []
for ville in meilleurePopulation.circuit:
lons.append(ville.lon)
lats.append(ville.lat)
noms.append(ville.nom)
lons.append(lons[0])
lats.append(lats[0])
noms.append(noms[0])
map = Basemap(llcrnrlon=-5.5,llcrnrlat=42.3,urcrnrlon=9.3,urcrnrlat=51.,
resolution='i', projection='tmerc', lat_0 = 45.5, lon_0 = -3.25)
map.drawmapboundary(fill_color='aqua')
map.fillcontinents(color='coral',lake_color='aqua')
map.drawcoastlines()
map.drawcountries()
x,y = map(lons,lats)
map.plot(x,y,'bo', markersize=12)
for nom,xpt,ypt in zip(noms,x,y):
plt.text(xpt+5000,ypt+25000,nom)
map.plot(x, y, 'D-', markersize=10, linewidth=2, color='k', markerfacecolor='b')
plt.show()Notre algorithme n’est pas déterministe, il ne nous garantit pas non plus d’obtenir la solution optimale.
Sur les deux graphiques ci-dessous nous représentons la distance totale du meilleur circuit (km) en fonction du nombre de générations :
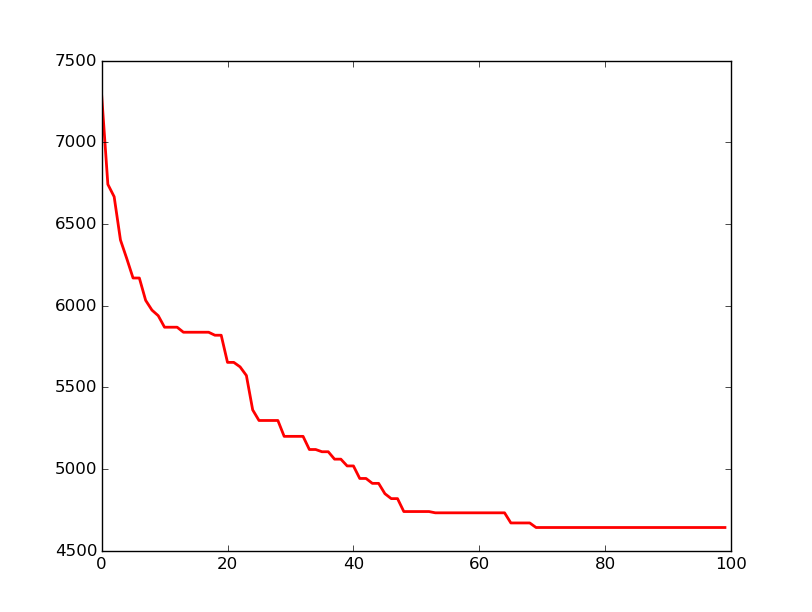On peut voir que notre solution s’améliore au fur et à mesure des générations. En effet, nous avons commencé avec un circuit d’une distance totale d’environ 7200km et nous finissons avec un circuit d’environ 4700 km.
Si nous relançons le programme, nous obtenons une meilleure solution, ce qui montre bien le non déterminisme de notre algorithme :
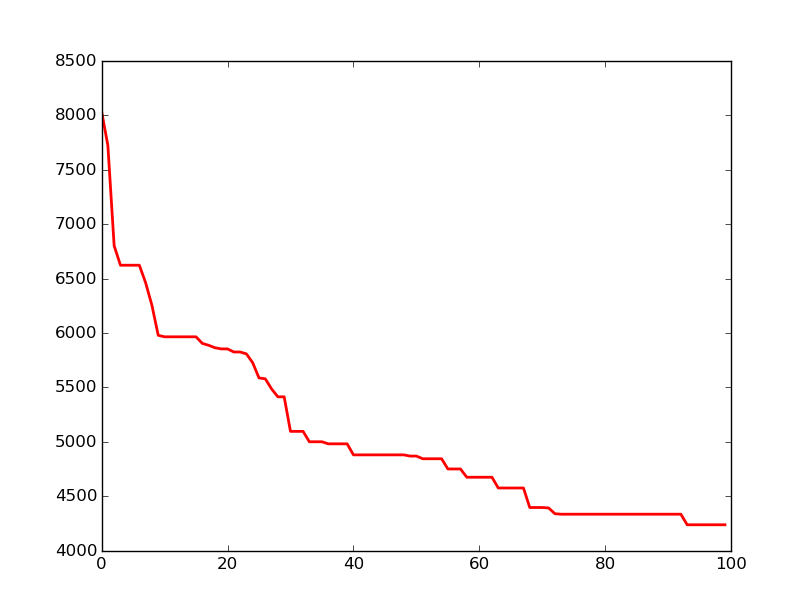
Nous avons représenté une de nos solutions en utilisant la librairie Basemap :
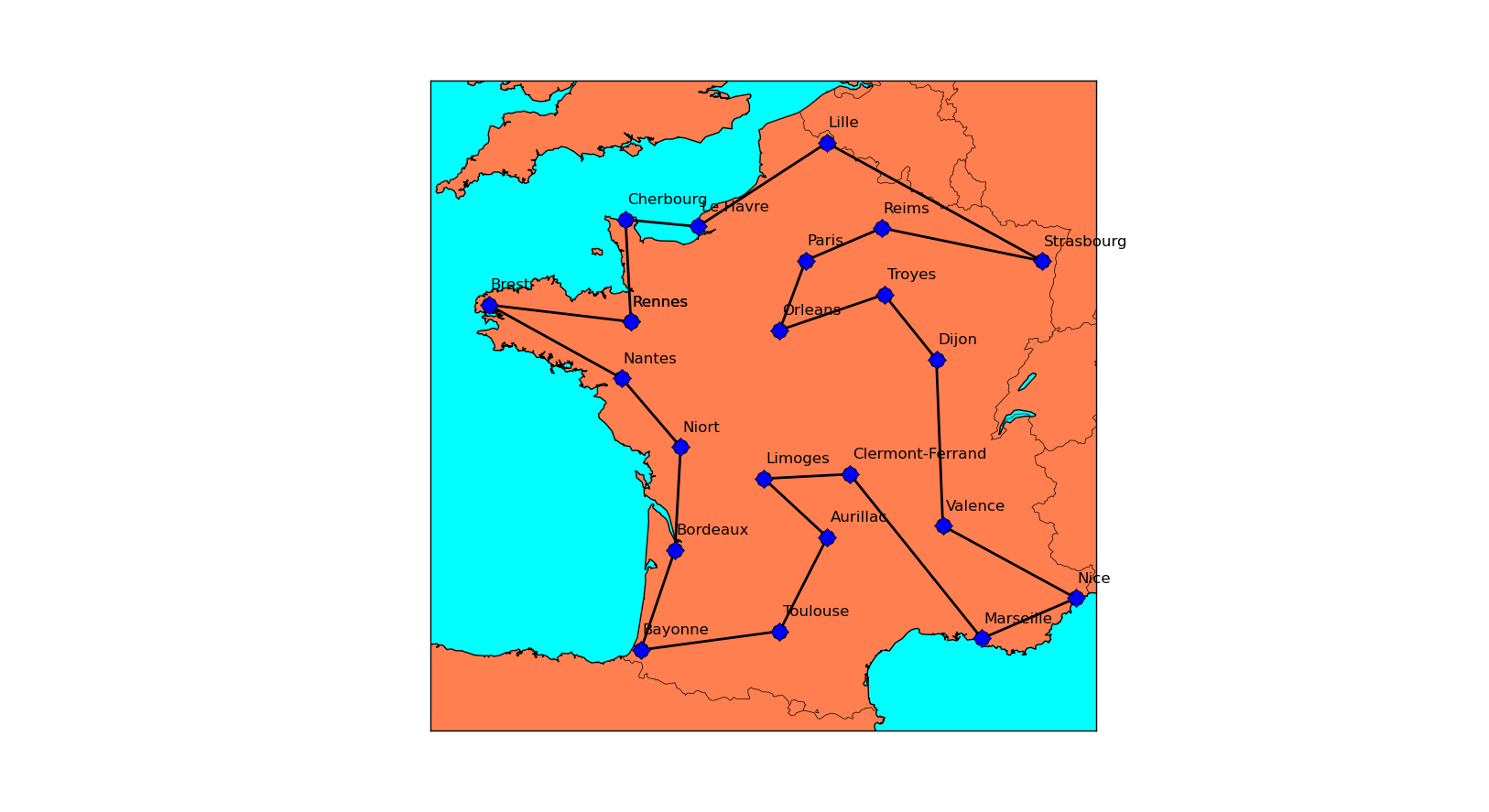
Comme vous pouvez le voir sur la carte, nous avons fait l’hypothèse que nous nous déplacions en ligne droite entre les villes, ce qui explique pourquoi nous traversons la mer entre Cherbourg et le Havre.
Nous pouvons également nous demander pourquoi nous nous contentons d’une solution bonne, mais qui n’est pas forcément optimale. La raison vient du fait que le problème du voyageur de commerce est un problème NP complet comme nous l’avons énoncé au début de cet article. Si vous vouliez aborder le problème de manière naïve en énumérant toutes les solutions, sachez que le nombre de chemins à tester explose de manière combinatoire ( 1/2*(n-1)!).
A titre d’exemple, avec 3 villes nous avons seulement 1 chemin à tester. Avec 9 villes nous avons 20160 chemins, et avec 20 villes plus de 6*10^16 chemins.
